Babylonian ‘algebra’ from Crest of the Peacock

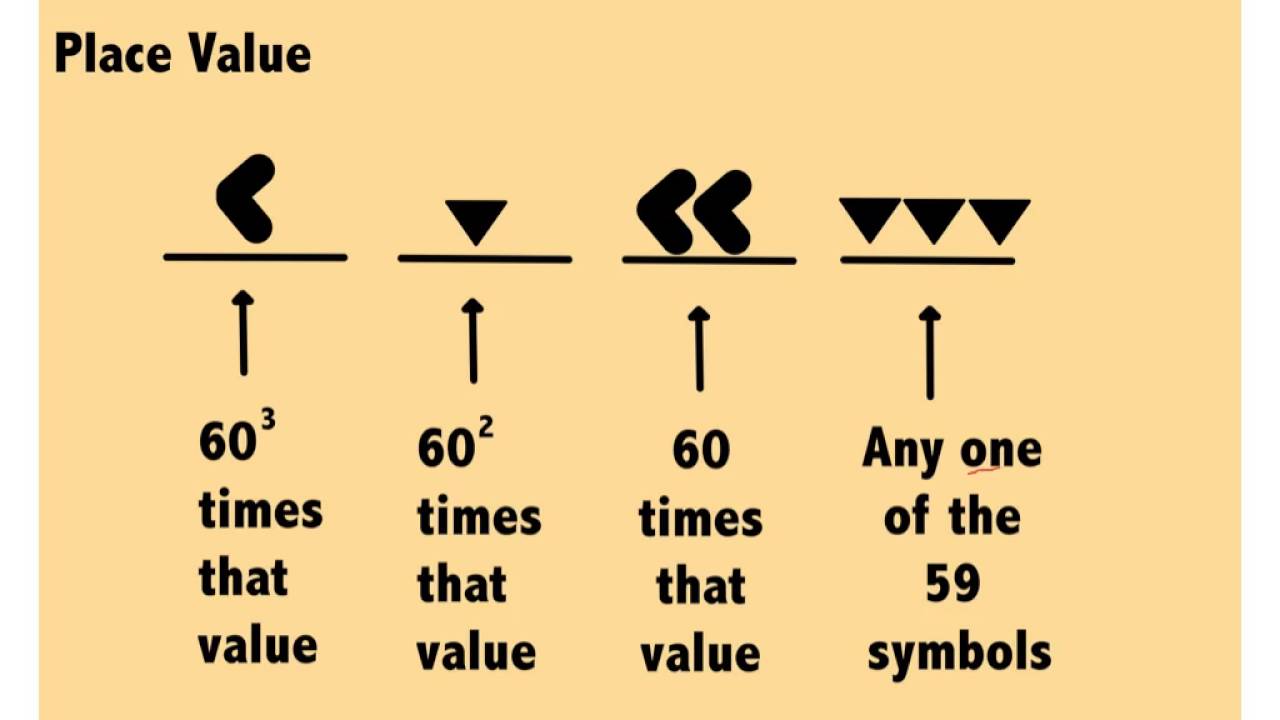
Image source: https://www.relativitycalculator.com/X-Cart/images/category/old_babylonian_mathematics_thumbnail.png

I think generalizations before the use of algebra would have been similar to the descriptions found in the reading. For example, the part stating, "I have subtracted the side of the square from the area..." uses words in place of variables. To generalize this further, the answer could simply be "the result," meaning the whole equation would be "Subtract the side of the square from the area to obtain the result" to represent modern day x² - x = y. 

I don't think math is all about generalization but there are benefits to both methods. For example, concise/algebraic notation allows us to focus on the calculation. The downside to this is we can lose sight of what it is we're actually doing through those calculations (which brings to mind the Bollywood song lyrics that translate to "There's confusion everywhere, and no solution in sight. Now, I've finally found the solution but who knows what the question was"). If the question isn't translated back and forth from algebra correctly, we can end up with incorrect results. If we use descriptions or key words while solving, we have a concrete understanding of what we're doing at each step, but the extra writing can become cumbersome and make the actual calculation difficult. The additional clutter can also be distracting.

I think descriptions could be used as alternate methods to algebra in lower level math, but eventually using keywords would be preferred. For example, in Pythagoras, a description could look like:

[one of the smaller sides of the right triangle squared] added to [the other smaller side of the right triangle squared] gives [the longest side of the right triangle squared]

To replace this description, we could have

[leg squared] added to the [other leg squared] results in [longest side squared] 

This would be slightly more manageable, as long as "leg" and "longest side" were defined correctly and universally understood. Something like calculating slope is still sort of taught this way with "rise over run." It's not overly descriptive but still uses word substitutions to obtain understanding before introducing Δy/Δx. 

As concepts get more difficult, however, descriptions and even keywords would get harder to balance. I think the excess clutter would make things harder to understand. Thinking of partial differential equations, it would be very difficult to keep everything in order without a compact notation. It would be longer and create more confusion when trying to decipher what calculations were taking place between each line of work.

Base 60 Multiplication Table for 45

My process

Base 60 Multiplication Table for 45:

Col.I		Col.II
1,15		36
2,5		21,36
4		11,15
6		7,30
7,12		6,15

2,5 x 21,36 second attempt:

George Joseph's Crest of the Peacock

Image source: http://img.auctiva.com/imgdata/5/0/2/1/4/6/webimg/398850408_o.jpg

One of the overall things that surprised me about this reading was the extent to which math development overlapped. The existence of the Bait al-Hikma (House of Wisdom) in Baghdad was particularly intriguing to me. The fact that a library containing Indian, Babylonian, Hellinistic, and possibly Chinese knowledge existed as early as the late 700s, and would go on to be the institution from which al-Khwarizmi would publish two books so influential to mathematics was new to me. I had initially thought math developed more or less in isolation until those branches met when travel became more prominent but I hadn't realized how early different civilizations began collaborating and influencing one another in this field. 

I also found it interesting that Buddhist pilgrimages were what really started the exchange of science and culture between China and India. In this case, I actually thought there would be more interactions between the two regions for trading purposes (which again exposes how little I know about the history of the world on a whole!). As well as the exchange of math, I would be interested to know the extent to which the two had cultural influences over one another (in my own time, of course!)

The achievements of Mayan civilization was another thing that surprised me. In particular, their accuracy in astronomy without the use of optic devices or a clock of some sort is mystifying. Looking at it with the knowledge we have today, it seems inconceivable that they were able to make astronomical discoveries with the level of accuracy that they achieved. I also wonder if this could be a case of artifacts lost or destroyed over time. If not, I wonder how they managed to do it!

Base 60 Homework

Image source: https://i.ytimg.com/vi/FxTencmpDLc/maxresdefault.jpg

1) When I first began thinking about base 60, all I could really come up with was that 60 is divisible by many numbers. It has 12 factors while 10 has 4 so it would be more convenient for division. However, this made me question why that would be significant. I realized I didn't know a lot about the historical and cultural context of the Babylonian people as more questions came to mind. What were they needing to count? How was 60 related to time? I wasn't sure how they were measuring time so I wasn't sure if they counted 60 seconds in a minute etc. What type of currency did they use (if they did) and how would counting by 60 be connected to that? How did they measure distance? Were they concerned with speed? I also wondered if the choice may have had something to do with the frequency of full moons, which are about every 29-30 days. I had all these questions but absolutely no idea because I hadn't really thought about it before, and I couldn't make educated guesses because I lacked the background information about Babylonian civilization.

2) The obvious connection with modern times was time (60 minutes in an hour, 60 seconds in a minute). I wasn't able to come up with many other ideas except maybe 60 miles/hour being a speed limit in the States but Imperial units aren't actually in base 60 so that isn't really related. I wasn't familiar with the Chinese zodiac system and couldn't think of any systems across other cultures either.

3) When I began my research, I looked for general knowledge about the significance of base 60 in Babylonian and other cultures. 60 being divisible by many numbers was a contributing factor to why they chose that system, but not in the way I had expected. In an article by O'Connor and Robertson, they describe how Babylonians used a table of reciprocals to multiply. The Babylonians used approximations for numbers that were not divisible so, as O'Connor and Robertson describe, if the fraction 1/13 was used, they would say 7/91 ~ 7 x 1/90, and indicate an approximation was used here. Thus, there was clearly an advantage to have a base with a high level of divisibility so less approximations would have to be made. Aside from that, 60 was also significant because the Babylonians devised the system of splitting the day into 24 hours with 60 minutes per hour and 60 seconds per minute. They represented these times with fractions to account for minutes and seconds (O'Connor and Robertson, 2000).

In terms of other uses of base 60, the Chinese Sexagenary Cycle is another ancient one. This time and space system consists of 10 heavenly stems and 12 earthly branches. A year consists of one heavenly branch and one earthly branch. The heavenly branch and earthly branch change sequentially each year (i.e. 1-1, 2-2 ... 1-11, 2-12, 3-1...10-12) until they reach the 60th year (10-12), at which point the cycle restarts. Base 60 has also been used by others in history including Plato's musical marriage allegory which involves the number 60^4 = 12 960 000, and by astronomers throughout history (see list on Wikipedia). One of the major points I missed was that 60 is a significant number in geometry with regards to angles. I was quite annoyed with myself for not thinking of that!

Blog Post #1: Why teach math history?

Image source: https://i.ytimg.com/vi/2No_CMrxBe8/maxresdefault.jpg

Prior to reading the article, I believed it was important to incorporate math history into my own math teaching. The reason for this is that I believe incorporating math history increases the chance that students might connect with the material being taught. When there’s a story to go along with it, they may understand how the concept came to be, why it was important at the time and why it is still used today. Alternatively, the student may just like an anecdote about the mathematician who discovered a formula, algorithm etc. In my opinion, anything that draws a student nearer to math in any way is an important avenue to pursue.

The article itself included many interesting ideas that I would like to explore further. One of the points that resonated the most with me was to include material from different cultures, not only to provide a connection with students from that heritage, but also to build respect for different cultures in general. I had never thought of it in that light before because I was more focused on what could be done to bring prominent mathematicians from different cultures as role models that students from that culture could relate to. Another point that stood out to me was the concept of “teaching sequence” as opposed to historical sequence of events. Of course, the benefit to this method would be to provide a more straightforward introduction to a concept but what I wondered was if it defeated the purpose of introducing the history at all. In other words, wouldn’t students disengage if they realized that they weren’t moving through events as they happened in human history?

After reading the article, I had a stronger sense of how to incorporate math history into my lessons, and a shift in understanding of what it actually means to do so. Prior to reading, I was focused more on telling stories about prominent mathematicians and their contribution to the field but I realized that the evolution of concepts is another facet of history. In my opinion, it also seems to be a more useful and applicable one for in a classroom setting. One idea I would really like to try is the “prototype equation” method in which starting from basic forms of a formula or equation could help provide some context as to how the refined version came to be and what it actually represents. Another idea I’d like to try is having historical packages. From their description, they seem to have the potential to lead to interesting discussions as well as serve as a good activity to change up the regular class routine. One thing I wouldn’t like to try is the exploration of errors. I’m sure there are teachers out there that would be able to successfully lead a lesson or activity on this, but I myself find spending time on incorrect findings stressful and frustrating so I wouldn’t be able to inspire students to gain useful knowledge out of their exploration.

Hello!

 I look forward to learning the history of math with everyone!

A photo from my "history"